Bound State in Dirac materials

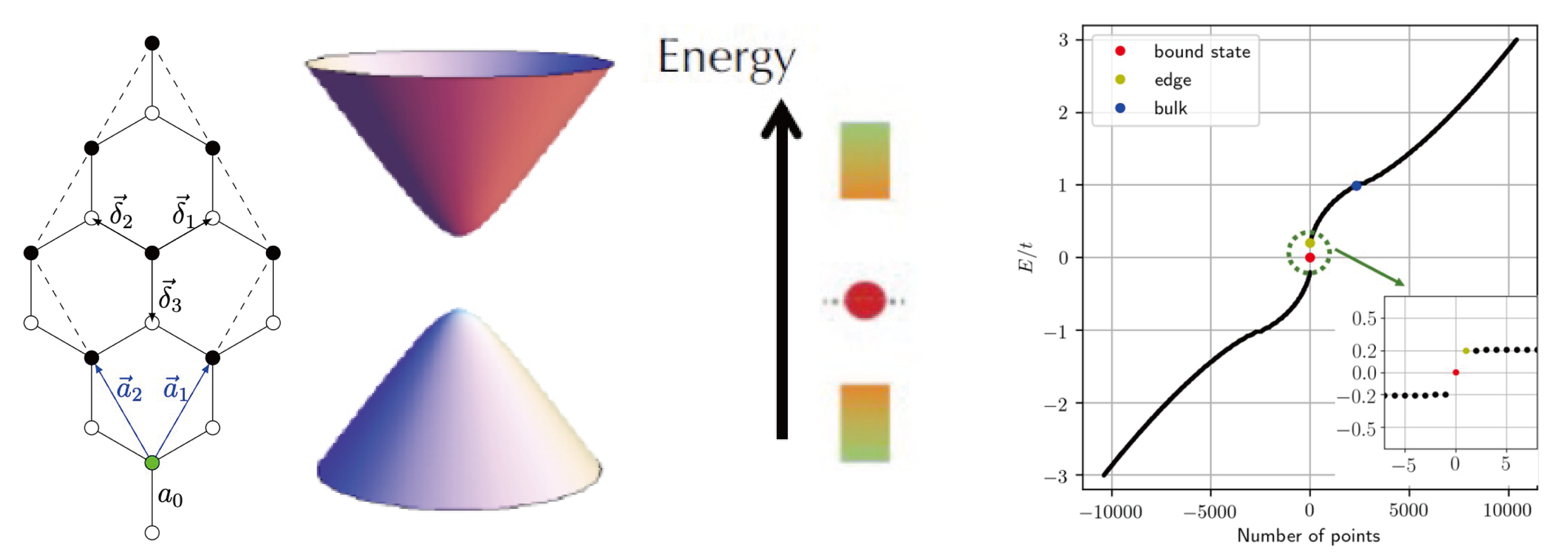
Description

This two-month internship project in 2022 served as a requirement to fulfil the first year of master at Université Paris-Saclay. Before that there was a research practice course I did in the same group in which I browsed through the literature of second quantization in non-relativistic quantum field theory, quantum many-body theory, and some literature about topological materials and topological phase transitions.

The internship work studies the bound state in gapped graphene system induced by an atomic impurity. It can be divided into two parts, the analytical part and the numerical part. For the analytical work, the local density of state (LDOS) for the gapless and gapped graphene was calculated by the Green function and T-matrix formalism. Existence of bound state for the latter is demonstrated. The numerical work begins by coding the tight binding Hamiltonian in Python from scratch. Certain features of the system established in analytic work were reproduced. In particular, the position of the bound state as a function of impurity strength computed by the numerics matches fairely well with the analytic prediction regularized by the atomic spacing with the correct geometric factor of the lattice. Attempts were made for establishing the expected wavefront dislocation for the bound states by numerical computation in the end. At the technical level, it might be better to just do a convolution in real space for filtering out certain momentum modes, instead of multiplying a Gaussian wavepacket in Fourier space and then inverse-Fourier transforming back, as is done in the report.

This work familiarized myself with the typical research style in theoretical condensed matter community: the combination of analytic and numerical calculations. The divergences in the field theoretic description are often regularized by Nature itself, i.e., the cut-off at lattice spacing. And then numerical computation can take over. Although I no longer work in this field, it’s good to keep this in my culture.

More details can be found in Internship report (2022).

The laboratory of Solid State Physics in Orsay, in the south subburb area of Paris